在嘗試建立模型時，我們要先預選一個方程式的基底形狀，這個方程式需要一定程度可以描述足夠多元的形狀，但什麼樣的 function 才是足夠好的 function，用一個 sin, cos 可以嗎？

到底 Activation Function 原先想要達成什麼目的，以此為契機所以才有後續這些方程式的選擇。

Activation Function

在第一次接觸 Activation Function 時，是以一個連續曲線，並以模型試圖去貼合的概念去理解：

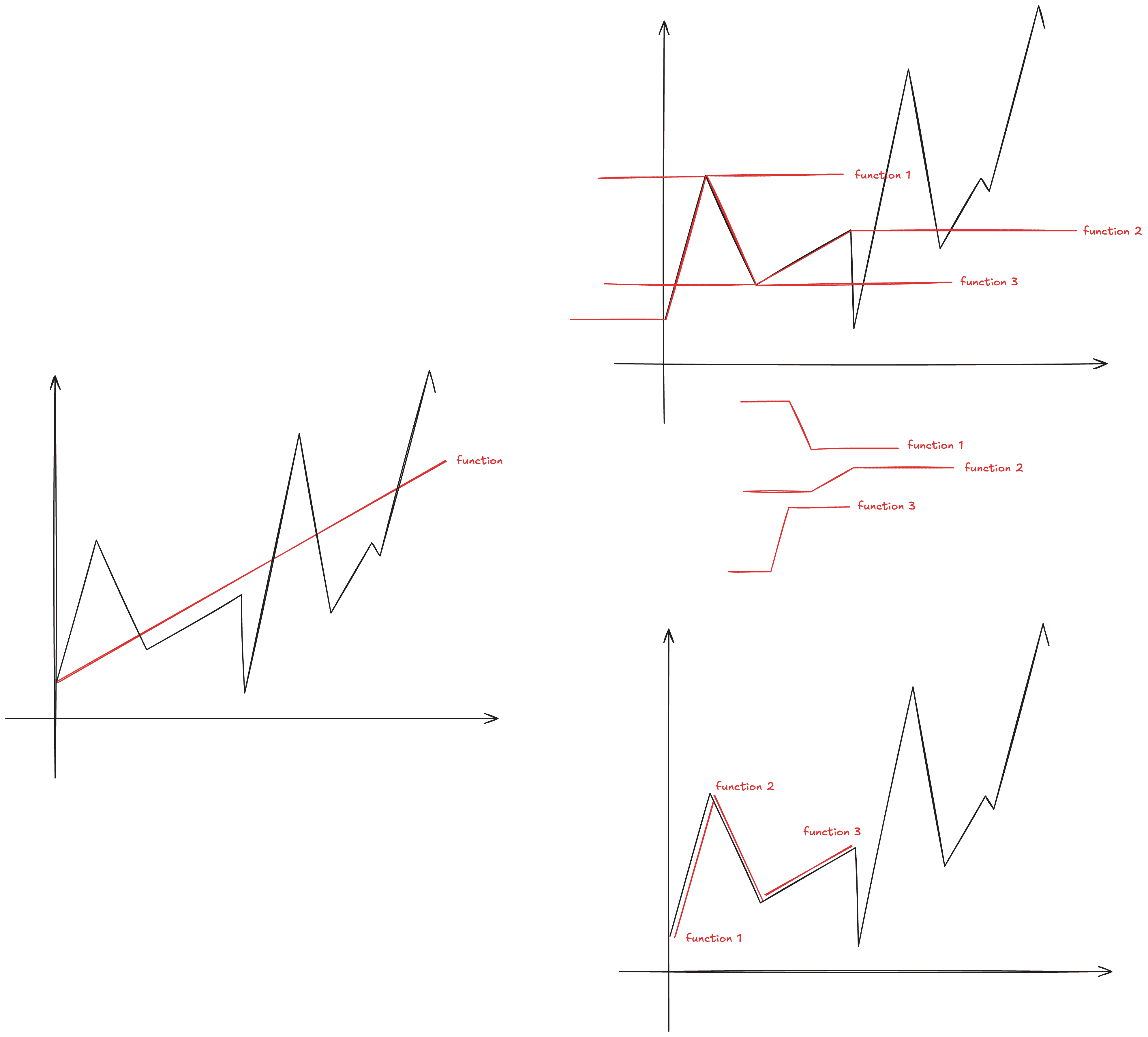
但從當時我就很納悶了，為什麼描述的 function 不能像下圖那樣是一段段 linear function 明明也是有機會一樣貼合？從圖面我只在意了要怎麼像是描圖的一樣表達出黑線的結果，但本質上，如果我要知道取哪一段線性方程式，在線性方程式中並沒有描述哪裡開始與結束的特質，這反而無法在數學上進行求解。

而實際上 activation 的命名揭露了，模型想要知道的，就是在什麼時候會開始傾斜，而從這個角度才比較掌握到 activation 的直觀意義。那這樣子的 activation 應該要有什麼特質：

• 非線性的：可以想像一個複雜模型如果全都以線性 function 來描述時，無法表現現實社會中充滿非線性的結果。

• x → y 的轉變要可用：可以把轉換關係想為座標系統上的一個曲線，如果今天 x 一改變，y 幾乎不會變（梯度非常不穩定）那這也不是一個好的 activation function 要有的樣子，那就好比 function 本身很難操作出斜率轉換的結果。

• 此 function 夠單純：可以看到完整的模型是透過複數個 function 去組合起來的，所以要能控制除了轉彎以外的地方，不會因為參數的浮動而跟著變動 e.g. cos, sin 也是有轉彎的 function，但他的參數一變整個 function 的波動都會跟著改變，這會影響其他部分的疊加。

Sigmoid

tanh

ReLU

GeLU